高校で習う三角比。有名なものにsin(サイン)、cos(コサイン)、tan(タンジェント)というものがあります。
実はこの3つ以外にも三角比は存在します!
また、三角比に関連したsin(サイン)、cos(コサイン)、tan(タンジェント)に似た記号(関数)もあります。これらは結構名前が似ていてややこしいので今回まとめてみました。

まずはsin, cos, tan
まずは、確認のためにsin, cos, tanの定義です。
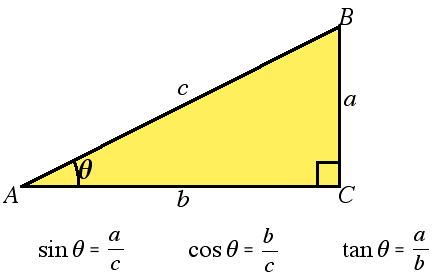
直角三角形ABCにおいて、角Aをθ、斜辺をcとすると、上の図のように
- sinθ=a/c
- cosθ=b/c
- tanθ=a/b
と定義されます。
それぞれ日本語では正弦、余弦、正接と言います。
他の三角比cosec, sec, cot
三角形には辺が3つあるわけですから、そこから2辺を選んでx/yのようなかたちで書く選び方は、
3×2 = 6通り
あります。sin, cos, tanで3通り出ていますから、残りは3通り。
それが、cose, sec, cotです。
- cosecθ=c/a (1/sinθ)
- secθ= c/b (1/cosθ)
- cotθ=b/a (1/tanθ)
式を見て分かるように、要するにsin, cos, tanの逆数です。
読み方は、cosecant(コセカント)、secant(セカント)、cotangent(コタンジェント)と言います。
日本語では、余割、正割、余接と言います。
逆関数のインバースやアーク
三角比の角度の部分を実数の変数にして定義される三角関数。その三角関数の逆関数を表すときに
- sin-1x
- cos-1x
- tan-1x
といったような書き方をし、インバース・サインなどと読みます。
でもこの書き方だと、うっかりすると1/sinxと勘違いしてしまう可能性があります。この混乱を避けるために、
- arcsinx
- arccosx
- arctanx
と書いて、アークサインなどと読みます。
双曲線関数になるとハイパボリックに
三角関数は双曲線関数と呼ばれる他の関数と類似性があります。
三角関数はテイラー展開すると、有名なオイラーの公式を使って、
![]()
![]()
と表すことができます。
一方で双曲線関数は非常によく似た形を使って、
![]()
上記のように定義される関数です。
それぞれ、ハイパボリックサイン、ハイパボリックコサインと読みます。
ただし、名前が長すぎるので、シャインやシンチ、コッシュなどと読まれることがあります。
いかがでしたか?
sin, cos, tanだけでなく三角比に関連する様々な関数や、統計学などにも知識を広げられてみてはいかがでしょうか?




コメント