数学的帰納法ってありますよね。
高校の数学で習うやつです。
具体的には、
k=nのとき成り立つと仮定したときに、k=n+1も成り立つことが示せたら、k=1で成り立つのなら全てのnで成り立つ…
といったやつです。
ものの考え方には帰納法の他に演繹法というのがあるのですが、数学的演繹法ってきいたことがないですよね?
それは一体なぜなのでしょう。
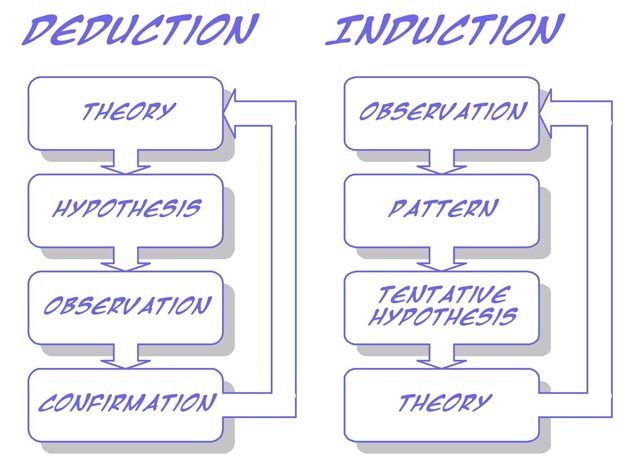
演繹法と帰納法って何?
そもそも演繹法と帰納法って何なのかということをまず見ていきたいと思います。
演繹法というのは、いわゆるAならばB、BならばC、よってAならばCといったようなものです。
論理的に考えれば、ある前提から結論まで、誰がやっても同じ結論に必ず達することができます。
例えば、
「犬は臭い」
「うちで飼っているペットは犬だ」
結論: うちで飼っているペットは臭い
といった感じのものです。論理的に考えれば、必然的に結論に達することができますね。
一方、帰納法というのは、必然的にというよりは、難しい言葉で言うと蓋然的に結論を導く方法です。
複数の観察で得られたものから一般則を導き出すようなときに使われます。
例えば、
「田中くんの家の犬は臭い」
「佐藤くんの家のネコは臭い」
「上杉くんの家の亀は臭い」
結論: 誰の家のペットも臭い
といったようなものです。
ここで見られるように、経験則というのも帰納的な考え方と言えますし、統計的考え方というのも帰納的です。
数学的演繹法がない理由
結論をいうと、数学は全部演繹法だからです。
足し算の計算方法を決めてしまえば、1+1は誰がやっても必然的に2になるように数学で扱う考え方は全て演繹的です。
そのため、帰納的な考え方をする、数学的帰納法のときだけわざわざ帰納法と呼んでいます。
しかもこの数学的帰納法ですら、仮説を導き出すときは帰納的な考え方をしますが、その後の証明は演繹法そのものです。
ただし、演繹的な考え方が多い数学であっても、この系統の問題だったら、こういう解き方でいけるんじゃないか?
などといった発想は経験から帰納的に考えだすものです。
ですので、数学でも演繹的な考え方と帰納的な考え方の両方を使いこなせるようになりましょう!
数学が得意な方には、ビジネスで活用できる統計学講座もオススメです!



コメント